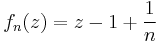Hurwitz's theorem (complex analysis)
In complex analysis, a field within mathematics, Hurwitz's theorem, named after Adolf Hurwitz, roughly states that, under certain conditions, if a sequence of holomorphic functions converges uniformly to a holomorphic function on compact sets, then after a while those functions and the limit function have the same number of zeros in any open disk.
More precisely, let  be an open set in the complex plane, and consider a sequence of holomorphic functions
be an open set in the complex plane, and consider a sequence of holomorphic functions 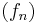 which converges uniformly on compact subsets of
which converges uniformly on compact subsets of  to a holomorphic function
to a holomorphic function 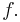 Let
Let 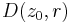 be an open disk of center
be an open disk of center 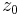 and radius
and radius  which is contained in
which is contained in  together with its boundary. Assume that
together with its boundary. Assume that 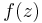 has no zeros on the disk boundary. Then, there exists a natural number
has no zeros on the disk boundary. Then, there exists a natural number  such that for all
such that for all  greater than
greater than  the functions
the functions 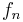 and
and  have the same number of zeros in
have the same number of zeros in 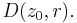
The requirement that  have no zeros on the disk boundary is necessary. For example, consider the unit disk, and the sequence
have no zeros on the disk boundary is necessary. For example, consider the unit disk, and the sequence
for all 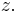 It converges uniformly to
It converges uniformly to 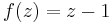 which has no zeros inside of this disk, but each
which has no zeros inside of this disk, but each 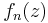 has exactly one zero in the disk, which is
has exactly one zero in the disk, which is 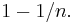
This result holds more generally for any bounded convex sets but it is most useful to state for disks.
An immediate consequence of this theorem is the following corollary. If  is an open set and a sequence of holomorphic functions
is an open set and a sequence of holomorphic functions 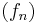 converges uniformly on compact subsets of
converges uniformly on compact subsets of  to a holomorphic function
to a holomorphic function 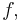 and furthermore if
and furthermore if 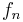 is not zero at any point in
is not zero at any point in  , then
, then  is either identically zero or also is never zero.
is either identically zero or also is never zero.
See also
References
- John B. Conway. Functions of One Complex Variable I. Springer-Verlag, New York, New York, 1978.
- E. C. Titchmarsh, The Theory of Functions, second edition (Oxford University Press, 1939; reprinted 1985), p. 119.
- Solomentsev, E.D. (2001), "Hurwitz theorem", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=H/h048160
This article incorporates material from Hurwitz's theorem on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.